n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
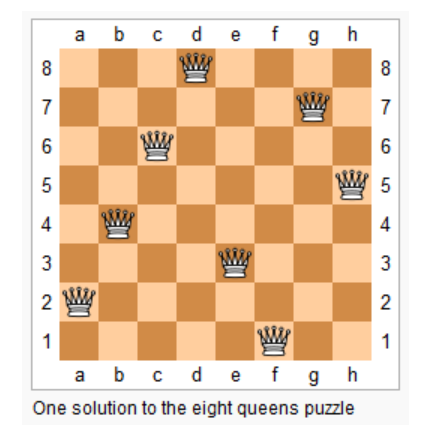
现在给定整数n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数n。
输出格式
每个解决方案占n行,每行输出一个长度为n的字符串,用来表示完整的棋盘状态。
其中”.”表示某一个位置的方格状态为空,”Q”表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
输出样例
1
2
3
4
5
6
7
8
9
10
| .Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
|
模板
第一种搜索方式
按格搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];
void dfs(int x, int y, int s)
{
if(y == n) y = 0, x ++;
if(x == n)
{
if(s == n)
{
for(int i = 0; i < n; i ++) puts(g[i]);
puts("");
}
return;
}
dfs(x, y + 1, s);
if(!row[x] && !col[y] && !dg[x + y] && !udg[n - y + x])
{
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[n - y + x] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[n - y + x] = false;
g[x][y] = '.';
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
for(int j = 0; j < n; j ++)
g[i][j] = '.';
dfs(0, 0, 0);
return 0;
}
|
第二种搜索方式
按行搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u)
{
if(u == n)
{
for(int i = 0; i < n; i ++) puts(g[i]);
puts("");
return;
}
for(int i = 0; i < n; i ++)
if(!col[i] && !dg[u + i] && !udg[n - u + i])
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false;
g[u][i] = '.';
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
for(int j = 0; j < n; j ++)
g[i][j] = '.';
dfs(0);
return 0;
}
|
